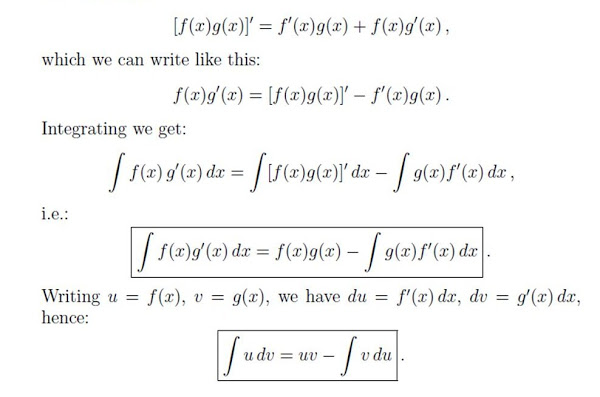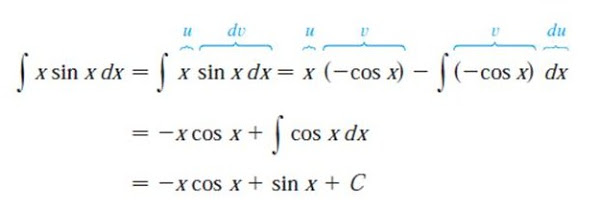We learned the fact that the Integration is the inverse of Differentiation. For Every differentiation rule there is a corresponding integration rule. Like the Substitution Rule for integration corresponds to the Chain Rule for differentiation. Now, the rule that corresponds to the Product Rule for differentiation is called the rule for integration by parts.
The Formula
The Steps
- The ability to choose u and dv correctly.
- If the choice is right, the new integral that you obtain is simpler than the original one.
- Integrate using the Integration by parts formula
- Check the answer by differentiating.
The Examples
1.
Let: u = x dv = ex dx
then: du = dx v = e
Solution:
Check by differentiating:
2.
Let: u = x dv = sin (x) dx
then: du = dx v = -cos (x)
Solution:
©2013 www.PinoyBIX.com
P inoyBIX educates thousands of reviewers and students a day in preparation for their board examinations. Also provides professionals with materials for their lectures and practice exams. Help me go forward with the same spirit.
“Will you subscribe today via YOUTUBE?”
TIRED OF ADS?
- Become Premium Member and experienced fewer ads to ads-free browsing.
- Full Content Access Exclusive to Premium members
- Access to PINOYBIX FREEBIES folder
- Download Reviewers and Learning Materials Free
- Download Content: You can see download/print button at the bottom of each post.
PINOYBIX FREEBIES FOR PREMIUM MEMBERSHIP:
- CIVIL ENGINEERING REVIEWER
- CIVIL SERVICE EXAM REVIEWER
- CRIMINOLOGY REVIEWER
- ELECTRONICS ENGINEERING REVIEWER (ECE/ECT)
- ELECTRICAL ENGINEERING & RME REVIEWER
- FIRE OFFICER EXAMINATION REVIEWER
- LET REVIEWER
- MASTER PLUMBER REVIEWER
- MECHANICAL ENGINEERING REVIEWER
- NAPOLCOM REVIEWER
- Additional upload reviewers and learning materials are also FREE
FOR A LIMITED TIME
If you subscribe for PREMIUM today!
You will receive an additional 1 month of Premium Membership FREE.
For Bronze Membership an additional 2 months of Premium Membership FREE.
For Silver Membership an additional 3 months of Premium Membership FREE.
For Gold Membership an additional 5 months of Premium Membership FREE.
Join the PinoyBIX community.